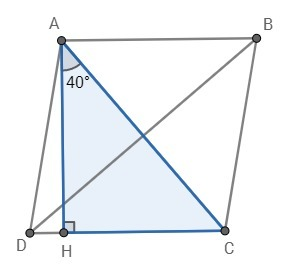
????????????????????????

Дано:
ABCD - ромб
АН - высота
∠НАС = 40°
Найти: ∠АDС; ∠АВС; ∠DАB; ∠DCB

Решение:
ΔНАС - прямоугольный (т.к. АН - высота)
∠АСН = 90° - ∠НАС = 90 - 40 = 50° (т.к. сумма острых углов прямоуг.Δ = 180°)
∠DCB = 2*∠АСН = 2 * 50 = 100° (т.к диагонали ромба являются биссектрисами его углов)
∠DАB = ∠DCB = 100° (т.к. противоположные углы ромба равны)
∠АВС = 180 - 100 = 80° (т.к. сумма соседних углов ромба = 180°)
∠АDС = ∠АВС =80° (т.к. противоположные углы ромба равны)

Ответ: ∠АDС = ∠АВС =80°; ∠DАB = ∠DCB = 100°