Каждая из трёх сторон трапеции в 2 раза меньше четвёртой стороны. Найти угол между диагоналями трапеции.
------
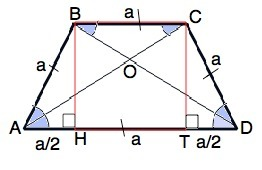
Обозначим трапецию АВСD.
По условию АВ=ВС=СD=0.5AD
Опустим высоты ВН и СТ. Тогда НТ=ВС=а
АН=ТD=a/2, т.к. трапеция равнобедренная.
В ∆ АВН катет АН=0,5 гипотенузы АВ.
cos∠BAH=AH:AB=0,5a:a=1/2. Это косинус 60°⇒
∠ВАН=60°
Треугольники АВС и ВСD равнобедренные, значит, их углы при основаниях АС и ВD равны.
Но ∠ВСА=∠САD и ∠CDВ=∠BDA как накрестлежащие.
Значит, BD и АС - биссектрисы. ⇒
∠ОАD=∠ODA=30°
Внешний угол треугольника ВОА при вершине О треугольника АОD равен сумме двух внутренних, не смежных с ним. ⇒
∠ВОА=30°+30°=60°