Найдем противоположное значение - вероятность промаха.
Этап 1 - найти вероятность попадания при одном выстреле.
Р(2) = p² + 2*p(1-p) = 0.91
Упрощаем и решаем квадратное уравнение.
p² - 2*p + 0.91 = 0.
Решение - D=0.36, √D=0.6
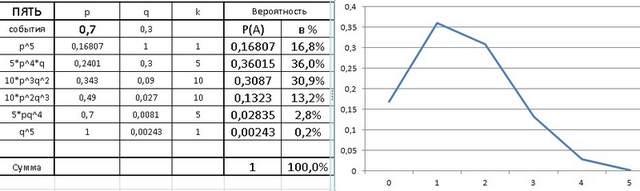
Вероятность попадания - p = 0.7 и промаха - q = 0.3 - для одного выстрела.
Этап 2 - п о формуле Пуассона
λ = n*p
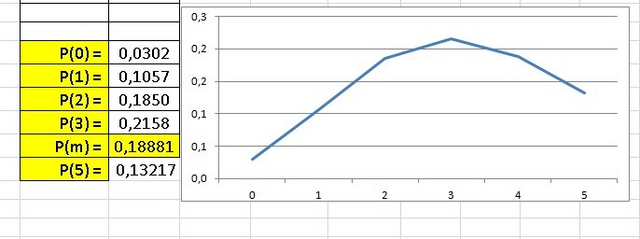
P(m) = λ^m* e^(-λ) / m!
n = 5, m=4, λ = n*p = 5*0.7 = 3.5 < 10 - можно продолжить расчет.
P(4) = 3.5⁴*e⁻³.⁵/4!
Предварительные расчеты
3.5⁴ =150.0625 , e⁻³.⁵ = 0.0302 и 4! = 4*3*2*1 = 24.
Р(4) =150.0625*0.0302:24 = 0.1881 - вероятность попадания - ОТВЕТ.
Функция распределения вероятности попадания - в подарок.
Более точно по формуле Полной вероятности