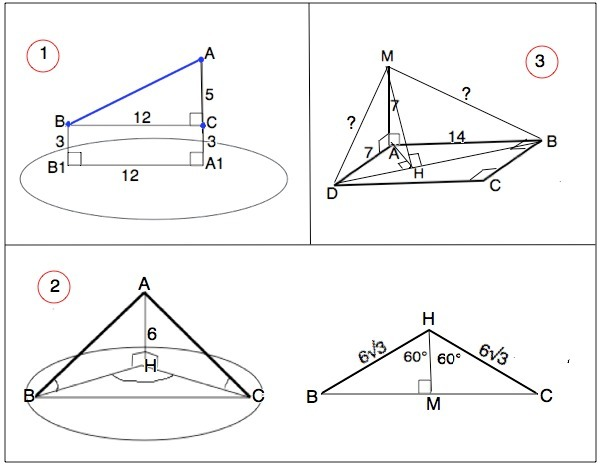
1)Концы отрезка, который не пересекает плоскость, отдалены от нее на 3 см и 8 см. Проекция отрезка на плоскость равна 12 см. Найти длину отрезка.
-----
Обозначим отрезок АВ. Расстоянием от точки до плоскости является длина отрезка, проведенного к ней перпендикулярно.
АА1 и ВВ1 перпендикулярны плоскости, следовательно, перпендикулярны В1А1.
АА1║ВВ1,
АВВ1А1 - прямоугольная трапеция.
ВВ1=3 см.АА1=8 см,
ВС║В1А1 ⇒ А1С=ВВ1=3 см, АС=8-3=5 см.
ВС=В1А1=12 см.
Катеты прямоугольного ∆ АВС относятся как 5:12 - треугольник из Пифагоровых троек, ⇒гипотенуза АВ=13 см.
* * *
2)Из точки, которая находится на расстоянии 6 см от плоскости, проведены две наклонные. Найти расстояние между основаниями наклонных, если угол между каждой наклонной и ее проекцией равен 30°, а угол между проекциями наклонных 120°.
-------
Наклонные АВ и АС, расстояние до плоскости АН=6 см, ∠АВН=∠АСН=30°
ВН=СН=АН:tg30°=6√3
∆АНС равнобедренный, угол ВНС=120° ( дано).
Проведем высоту НМ к основанию ВС. Высота в равнобедренном треугольнике - биссектриса и медиана. ⇒ ∆ ВНМ=∆ СНМ, ∠ВНМ=СНМ=60°
ВМ=ВН•sin60°=6√3•√3/2=9
BC=2•BМ=18 см (по т.косинусов ВС также равно 18 см)
* * *
3)Из вершины А прямоугольника АВСD со сторонами 7 см и 14 см к его плоскости проведен перпендикуляр АМ=7 см. Найти расстояние от точки М до прямых DС и DB.
--------
Примем АВ=14 см, АD=7 см. Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно от точки до прямой. По т. о 3-х перпендикулярах МD пп DC, МВ пп ВС.
В прямоугольном ∆ MAD катеты равны, следовательно, он равнобедренный с острыми углами, равными 45°.
MD=AD:sin45°=7√2.
Из прямоугольного ∆ МАВ расстояние МВ=√(AB²+AM²)=√(196+49)=7√5 см
Расстояние от М до BD отрезок МН, перпендикулярный диагонали ABCD.
По т. о 3-х перпендикулярах МН⊥DB,⇒ его проекция АН⊥DB.
АН=AD•AB:BD
∆ ADB=∆ MAB по двум катетам,⇒ DB=MB=7√5
AH=7•14:7√5=14/√5
MH=√(AM²+AH²)=√(441/5)=21/√5=4,2√5 или ≈ 9,39 см