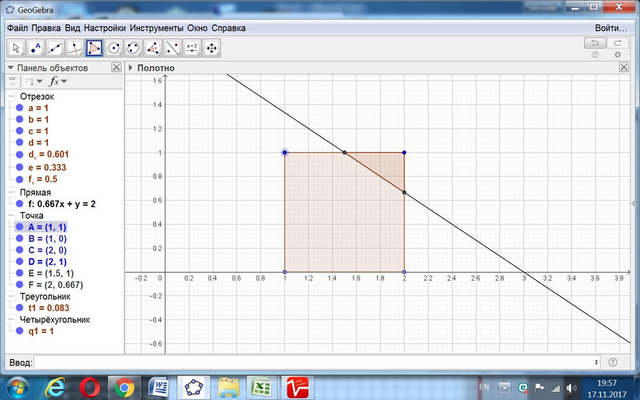
Уравнение прямой по условию задания (по координатам точек):
у = (-2/3)х + 2.
Квадрат имеет углы с координатами
- по оси Ох: х = 1 и х = 2.
- по оси Оу: у = 0 и у = 1.
Прямая пересекает 2 стороны квадрата, одну с у = 1, вторую с х = 2.
Находим координаты точек пересечения прямой и сторон квадрата.
1 = (-2/3)*х + 2, х = 3/2 = 1,5.
у = (-2/3)*2 + 2 = 2/3.
Отсюда получаем длины сторон прямоугольного треугольника:
по х: 2 - 1,5 = 0,5 = 1/2.
по у: 1 - (2/3) = 1/3.
Тогда S = (1/2)*(1/2)*(1/3) = 1/12 ≈ 0.08333 кв.ед.