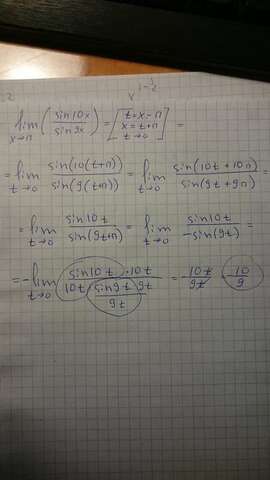Решение первого примера в приложении.
Чтобы решить этот предел мы можем воспользоваться первым замечательным пределом. Но, чтобы это сделать, x должен стремиться к 0. Для этого мы вводим новую переменную t = x - п. Так как х стремится к п, то t будет стремится к 0 (t = п - п = 0). Это то, что нам нужно.