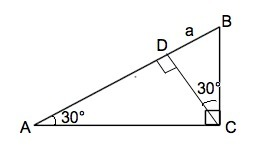
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные треугольники.
∆ АВС~∆ BCD,⇒ угол ВСD=30°.
В ∆ BCD катет DB противолежит углу 30°, значит, гипотенуза СВ=2•BD.
Аналогично в ∆ АСD гипотенуза АС=2•CD⇒
АС+ВС=2•(BD+CD)
AC+BC=2•2017=4034
–––––––––
Или, если нужны вычисления:
Примем ВD=a
Тогда CD=BD:ctg30=a√3
CD+BD=а(1+√3)
ВС=BD:sin30°=2а,
АС=ВС:ctg30=2a√3
АС+ВС=2а(1+√3) - вдвое больше BD+CD ⇒
АС+ВС=1017•2=4034