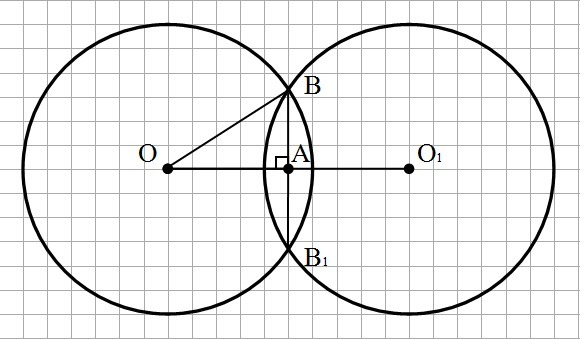
Расстояние между центрами окружностей L = 24 см.
Так как радиусы окружностей одинаковые, то расстояние от центра окружности до общей хорды:
ОА = ОО₁/2 = 12 см.
Получили прямоугольный треугольник с гипотенузой ОВ, равной радиусу окружности и катетами ОА и АВ, причем в ΔОАВ и ΔОАВ₁:
ОВ = ОВ₁ и ОА - общая => АВ = АВ₁ и ВВ₁ = 2*АВ
Тогда половина общей хорды (катет АВ треугольника):
ВВ₁/2 = AB = √(13²-12²) = √(169-144) = √25 = 5 (см)
И длина общей хорды:
BB₁ = 10 см
Ответ: 10 см