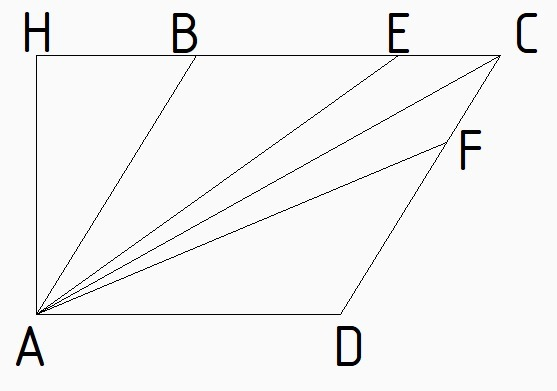
Прощадь ромба
S = a^2*sin(α)
Площадь каждой из трёх равновеликих фигур
S = a^2*sin(α)/3
Две фигуры - это треугольники АВЕ и AFD, третья - четырёхугольник AECF
Четырёхугольник AECF в свою очередь состоит из двух равных треугольников AEC и ACF
Значит площадь треугольника ABE в два раза больше площади треугольника AEC
AH - высота для треугольника ABE и треугольника AEC
АН = АB*sin(HBA) = AB*sin(BAD) = a*sin(α)
Т.к. высота для треугольника ABE и треугольника AEC общая, то их площади относятся как основания треугольников
и ВЕ = 2EC = 2/3a
По теореме косинусов
AE^2 = AB^2 + BE^2 - 2*AB*BE*cos(π-α) = a^2 + 4/9*a^2 + 2*a*2/3*a*cos(α) = 13/9*a^2 + 4/3*a^2*cos(α) = a^2*(13/9 + 4/3*cos(α))
AE = a*(13/9 + 4/3*cos(α))^(1/2)