1.Что я делал:
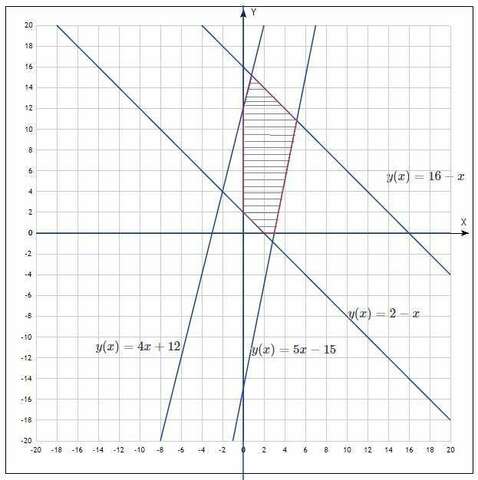
Обозначил x1 и x2 через x и y (просто так удобнее, можешь на рисунке их обратно заменить). Решал неравенства относительно y:
y≤16-x
y≥5x-15
y≤4x+12
y≥2-x
x≥0
y≥0
Дальше построил их графики. Там все прямые, поэтому они делят плоскость на 2 полуплоскости, одна из которых является решением неравенства (можно взять любую точку из полуплоскости, подставить в неравенство, если неравенство будет верным, то эта полуплоскость - решение неравенства, иначе другая полуплоскость - решение. Подставим точку (0;0) в первое неравенство 0≤16 - верно, то есть вся нижняя часть от y=16-x будет решением неравенства, в том числе и прямая (неравенство нестрогое), её заштриховываешь, делаешь то же самое с остальными прямыми и получаешь контур, как на рисунке). Всё, что внутри данного шестиугольника, а также сам шестиугольник - решение системы неравенств.
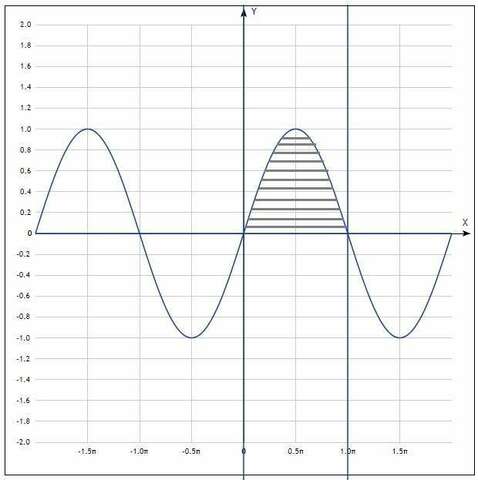
2. Тут всё понятно. Строим y=sin(x), можно построить прямые x=0; x=π, y=0, получаем фигурку, напоминающую колокол. Для вычисления площади находим интеграл