1. ДАНО Y(x) = 1/3*x³ -x²
Исследование на экстремумы.
1) Производная - Y'(x) = x² - 2x = x*(x-2).
2) Находим корни производной - Y'(x) = 0 при х1 = 0 и х2 = 2.
3) Экстремумы функции в корнях производной
Ymax(0) = 0 и Ymin(2) = 8/3 - 4 = - 1 1/3
Монотонность.
Возрастает - X∈(-∞;0)∪(2;+∞)
3. ДАНО Y= 1/3*
Убывает - X∈(0;2)
2. ДАНО Y= 1/4*x³ - 3*x² +2
Исследование на выпуклость.
1) Находим первую производную - Y'(x) = 3/4*x² - 6*x
2) Находим вторую производную - Y"(x) = 3/2*x - 6.
3) Находим корни второй производной - Y"(x) = 0.
3/2*x = 6
х = 6 : 3/2 = 4 - точка перегиба.
4) Выпуклая - "горка" - X∈(-∞;4)
Вогнутая - "ложка" - X∈(4;+∞)
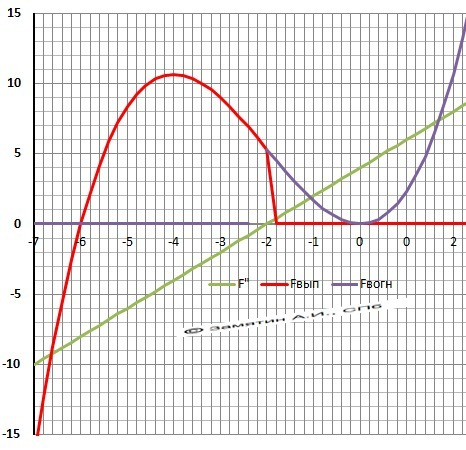
3. ДАНО Y = 1/3*x³ + 2*x²
ИССЛЕДОВАНИЕ.
1. Область определения - непрерывная. Х∈(-∞;+∞)
2. Область значений - Y(-∞;+∞)
3. Первая производная - Y'(x) = x²+4*x = x*(x+4)
4. Экстремумы. Y'(x)=0.
Ymax(-4) = 10 2/3 = 10.(6)
Ymin(0) = 0.
5. Вторая производная - Y"(x) = 2*x+4 = 2*(x+2)
6. Точка перегиба - Y"(x) = 0 при х = -2
7. Выпуклая - "горка" - X∈(-∞;-2)
Вогнутая - "ложка" - X∈(-2;+∞)
8. График в приложении.