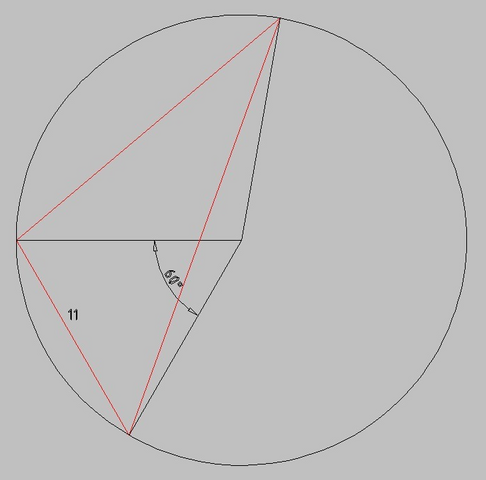
Длины дуг, на которые разбивается описанная окружность составляют 3x, 5x, 10x
3x + 5x + 10x = 360°
18x = 360
x = 20
центральные углы, опирающиеся на дуги равны
60°, 100°, 200°
Меньшей из сторон соответствует наименьший угол, 60°
Два радиуса и наименьшая сторона образуют равносторонний треугольник с углом при вершине 60° и основанием 11
Найдём его боковую сторону, по теореме косинусов
11² = r² + r² - 2·r·r·cos (60°)
11² = 2·r² - 2·r²·1/2
11² = 2·r² - r²
11² = r²
r = 11
Можно и проще, если угол при вершине треугольника 60°, то при основании тоже 60° и треугольник равносторонний, радиус равен стороне.