Девять прямых, параллельных одной из сторон треугольника , делят две другие стороны **...

Question

Девять прямых, параллельных одной из сторон треугольника , делят две другие стороны на десять равных частей каждую, а сам треугольник на маленький треугольник и девять трапеций. Площадь большей из этих трапеций равна 76 кв. см. Найдите площадь (в кв. см) треугольника.

Answer 1

Пусть площадь самого маленького треугольничка равна 
S₁= 1/2 a*h
a - основание маленького треугольничка
h - его высота
Следующий треугольник будет обладать в два раза большим основанием и в два раза большей высотой.
S₂= 1/2*2a*2h=2ah
Третий треугольник имеет в 3 раза большую высоту и в три ваза большее основание
...
Девятый имеет в 9 раз большие размеры
S₉= 1/2*9a*9h=40,5*ah
Десятый, это, собственно, сам исходный треугольник имеет в 10 раз большие размеры
S₁₀= 1/2*10a*10h=50ah
Площадь самой большой трапеции равна S₁₀-S₉ = 9,5ah
9,5ah = 76
ah = 76/9,5 = 8 кв см
И площадь большого треугольника
S₁₀ = 50ah = 400 кв.см.

Answer 2

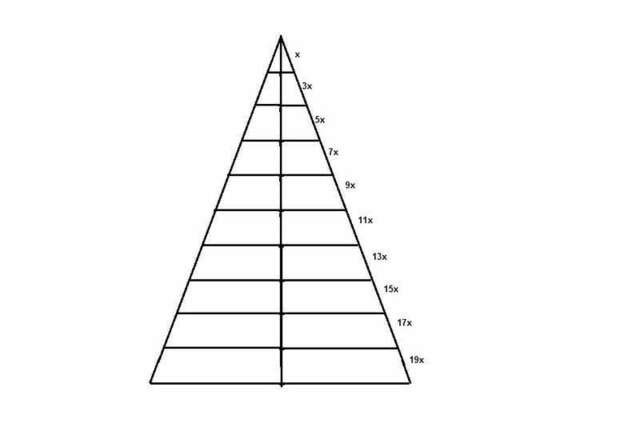
Вот на рисунке показан этот треугольник с 9 линиями.
Пусть верхний треугольник имеет площадь х кв.см.
Рассмотрим два верхних треугольника.
Очевидно, что первая линия - средняя для второго треугольника.
Высота первого треугольника в 2 раза меньше, чем у второго.
Основание тоже в 2 раза меньше. Значит, второй треугольник имеет площадь 4x, а трапеция - площадь 3x.
Рассуждая точно также, получаем, что третий треугольник имеет высоту и основание в 3 раза больше, чем первый. Его площадь 9x, а площадь трапеции 9x - x - 3x = 5x.
Таким образом, площади трапеции - это нечетные коэффициенты при x.
10-ый треугольник будет иметь площадь 100x, потому что его основание и высота в 10 раз больше, чем у первого треугольника.
Площадь 10-ой трапеции будет 19x, и мы знаем, что она равна 76 кв.см.
Уравнение: 19x = 76, отсюда x = 4 кв.см. - площадь первого треугольника.
Площадь большого треугольника равна 100x = 400 кв.см.

---