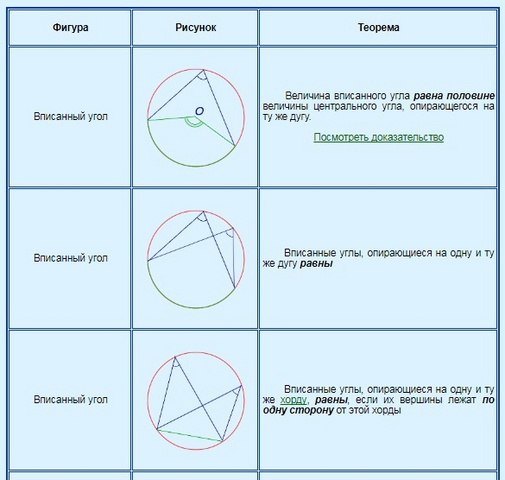
1. ∠АОС - центральный, ∠АВС - вписанный. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
∠АВС = 80/2 = 40°
2. Аналогично первому, но наоборот.
36*2 = 72°
3. Оба угла - вписанные, опираются на одну дугу. Значит, они равны.
36°
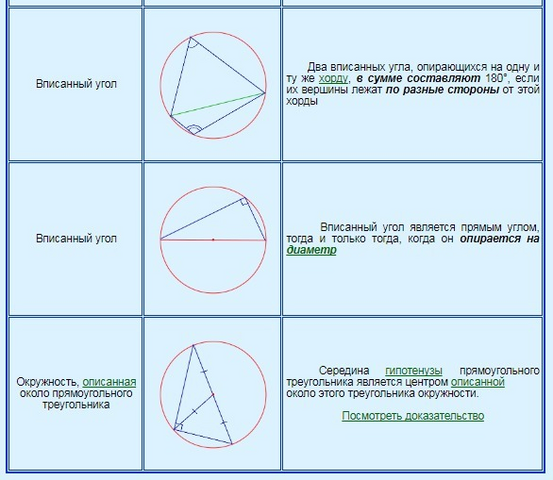
4. Если гипотенуза треугольника, вписанного в окружность, опирается на диаметр, значит, этот треугольник - прямоугольный. Таким образом, ∠АВС = 90°. Зная, что ∠АВС=90° и ∠АСВ=40° (из дано), найдем третий угол в треугольнике АВС:
∠САВ = 180-90-40 = 50°
∠САВ и ∠СDB - вписанные и опираются на одну дугу, а значит, оба равны 50°.
5. Доказывай, опираясь на выше затронутые теоремы.