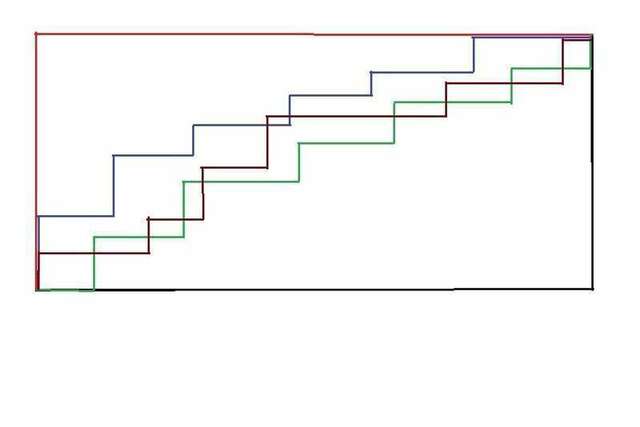
1) Чтобы быстрее попасть в нужную точку (314, 271) из точки (0, 0), нужно ходить только вправо и вверх.
Вправо нужно сдвинуться на 314, а вверх на 271 клетку.
Всего он сделает 314 + 271 = 585 ходов.
И неважно, как он будет идти: сначала только вправо, потом вверх, или наоборот, сначала вверх, а потом вправо, или вообще вправо и вверх через раз, то есть по диагонали. Вот я нарисовал несколько путей.
2) 90531 - 87642 = 2889