Ребята две супер задачи,можете решить и объяснить?(советую решить в тетради и...

Question

Ребята две супер задачи,можете решить и объяснить?(советую решить в тетради и сфоткать,задачи одниз из длинно решаемых задач)

---

Answer 1

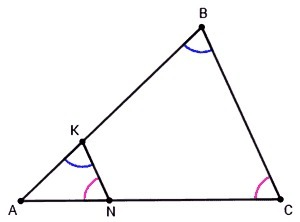
∠AKN=∠B, ∠ANK=∠C (соответственные углы при KN||BC)
△AKN~△ABC (по двум углам)
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(AKN)/S(ABC) =k^2 <=> S(AKN)= S(ABC)*(AK/AB)^2

36) S(AKN)= 18*(1/3)^2 =18/9 =2

37) S(AKN)= 16*(1/2)^2 =16/4 =4

ИЛИ
По теореме Фалеса параллельные прямые отсекают пропорциональные отрезки:
AK/AN =AB/AC <=> AK/AB =AN/AC
S(AKN)= (AK*AN*sinA)/2
S(ABC)= (AB*AC*sinA)/2
S(AKN)/S(ABC) =AK*AN/AB*AC =(AK/AB)^2 <=> S(AKN)= S(ABC)*(AK/AB)^2

---

Comments

Чувак у тебя решение классное и очень быстрое,но можешь ли решить без подобия треугольника?