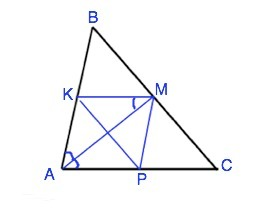
По условию отрезки КМ║АС, и МР║АВ.
Четырёхугольник, у которого противоположные стороны попарно параллельны, является параллелограммом
В параллелограмме КМРА диагональ АМ - секущая при КМ║|АР, поэтому накрестлежащие ∠КМА=∠МАР.
Так как АМ биссектриса, то ∠КМА=∠КАМ, и ∆ АКМ - равнобедренный.
Аналогично доказывается, что ∆ АРМ равнобедренный.
Если стороны параллелограмма равны, этот параллелограмм - ромб.
Диагонали ромба – - биссектрисы, медианы и высоты равнобедренных треугольников, образуемых ими с соседними сторонами ромба. ⇒
Диагонали ромба взаимно перпендикулярны.