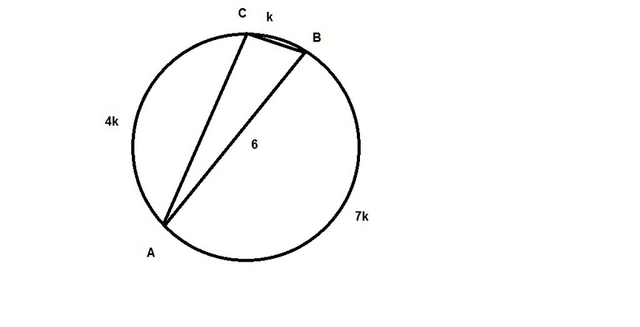
Пусть k - коэффициент пропорциональности. Тогда дуги, на которые вершины треугольника делят окружность, равны k; 4k; 7k. Т.к. градусная мера всей окружности равна 360°, то
k+4k+7k=360
12k=360
k=30
Вписанный угол равен половине дуги, на которую он опирается:
∠A=30/2=15°
∠B=4*30/2=2*30=60°
∠C=7*30/2=7*15=105°
По теореме синусов:
AB/sinC=BC/sinA=AC/sinB
6/sin105°=BC/sin15°=AC/sin60°
BC≈1,6
AC≈5,4
Ответ: ∠A=15°; ∠B=60°; ∠C=105°; BC=1,6; AC=5,4