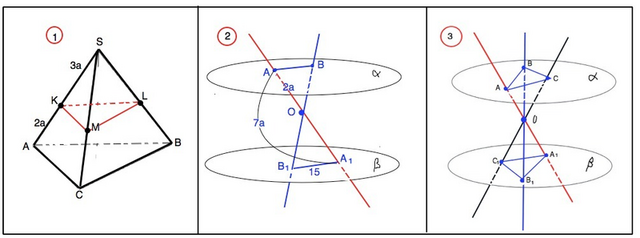
1)
На ребрах SA, SB, SC тетраэдра SABC выбраны точки К, L и М так, что SK:KA+SL:LB=SM:MC. Докажите, что плоскости мКL и АВС параллельны. Найдите площадь треугольника АВС, если площадь треугольника КLM равна 15 см и SK:KA=3:2
-------------------
Грани тетраэдра - треугольники. Плоскость КLM "отсекает" на их сторонах пропорциональные отрезки. Следовательно, КМ||АС, ML||CB, KL||AB
КМ и МL, АС и СВ пересекаются в своих плоскостях и параллельны. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Стороны треугольников КLM и АВС параллельны, значит, углы, заключенные между сходственными сторонами равны. Треугольники КLM и АВС подобны по равным углам. Из отношения SK:KA=3:2 коэффициент подобия КМ:АС=SA:SK=5:3
Отношение площадей подобных фигур равно квадрату коэффициента подобия. S KLM:S ABC=9:25⇒
25•15=9 SABC ⇒ S (ABC)=41 ²/₃
------------------
2)
Через точку О. расположенную между параллельными плоскостям альфа и бета проведены две прямые. Они пересекают плоскость альфа в точках А и В, плоскость бета – в точках А1 и В1 Вычислите длину отрезка АВ, если А1В1=15 см, АА1:ОА=7:2
Прямые АА1 и ВВ1 пересекаются. Через пересекающиеся прямые можно провести плоскость, притом только одну. Эта плоскость пересекает с плоскости α и β по параллельным прямым (свойство) . АА1 и ВВ1 секущие при параллельных АВ| и А1В1. Накрестлежащие углы при этом равны.
Треугольники АОВ и А1ОВ1 подобны по трем углам. Примем коэффициент подобия равным а. АА1=7, АО=2 ⇒ ОА1=7а-2а=5а.
Тогда АО:ОА1=2:5, и АВ:А1В1=2:5
5АВ=2А1В 5 АВ=30⇒ АВ=6
-----------------
3)
Через точку О, расположенную между параллельными плоскостями а и б, проведены три прямые, которые пересекают эти плоскости в А, А1, В, В1 и С,С1 соответственно. Найдите стороны треугольника А1В1С1, если его площадь 336 см² и АВ=13 см, СВ-14 см. АС=15 см.
Через пары пересекающихся прямых АА1 и ВВ1 и других пар можно провести по одной плоскости, каждая из которых пересекает плоскости α и β по параллельным прямым.
Стороны треугольников АВС и А1В1С1 параллельны, эти треугольники подобны. Площадь ∆ АВС по ф. Герона равна 84 ( сочетание сторон такой длины в треугольниках так часто встречается, что их площадь поневоле запоминается)
Отношение площади А1В1С1 к площади АВС 336:84=4.
Отношение площадей подобных фигур равно квадрату коэффициента подобия. ⇒k=√4=2.
Стороны треугольника А1В1С1= 13•2=26 см; 14•2=28 см; 15•2=30 см