СРОЧНО!!!!!!!!!!! 1. Береговые радиомаяки А и В расположены ** расстоянии 10 км. С судна...

Question

СРОЧНО!!!!!!!!!!!
1. Береговые радиомаяки А и В расположены на расстоянии 10 км. С судна С с помощью находящейся на ней радиолокационной станции, определены расстояния до маяков СА=11 км и СВ=9 км. Найдите углы САВ и СВА пеленгов радиомаяков. В ответ запишите градусную меру наибольшего из этих углов.
2. Дан правильный многоугольник и длина радиуса R окружности описанной около многоугольника. Определи площадь многоугольника, если: - у многоугольника 8 сторон и R=10 см (если корня в ответе нет, под знаком корня пиши 1) - у многоугольника 10 сторон и R=10 см (ответ округли до целых)

Answer 1

Задача 1.
В решении используется теорема КОСИНУСОВ для треугольника.
ДАНО
a = 10 км
b = 11 км
c = 9 км
НАЙТИ -  углы
РЕШЕНИЕ
с² = a² + b² - 2ab*cos α
Отсюда α
α = arccos((a²+b²-c²)/(2*ab)
Меняем точку отсчета - (A или В или С) и получаем косинусы углов:
А = 0,5152 и В = 0,4 и С = 0,6363
 - ответы
∠А = 58,9
∠В = 50,48
∠С = 70,13
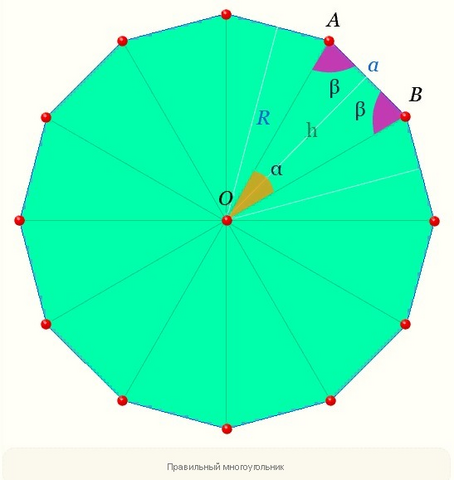
Задача 2.
Вариант 1) n = 8, R=10.
Формула площади многоугольника:
S= 1/2 *n*h*α 
α= 2π/n = 0.785 рад = 45 град - центральный угол
h = R*cos(α/2) = 10*cos(0,3927) = 10*0.9238 = 9.238 см - апофема - высота треугольника.
Подставили и получили 
S = 1/2*n*h*α = 36.955 см² - площадь восьмиугольника - ОТВЕТ 1
Вариант 2) n = 10, R = 10 см.
α = 36° = 0,6283 рад.
cos(α/2) = 0.951
S = 47.552 - см² - ОТВЕТ
Расчет в действительных числах.

---

Comments

а второе?

---

8 или 10 сторон - это не 4 или 6. Формулы сложные, а изменить ответ можно только один раз. Подожди немного.