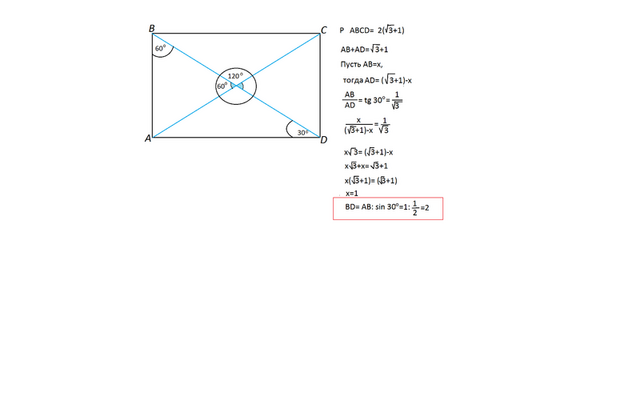
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
Следовательно, половины диагоналей и каждая из сторон образуют равнобедренные треугольники.
Диагонали образуют при пересечении 2 угла.
Один из них равен по условию 60 градусов.
Равнобедренный треугольник, в котором угол при вершине равен 60 градусов, является равносторонним.
Обозначим вершины прямоугольника ABCD
Диагональ BD и стороны AB и AD прямоугольника образуют прямоугольный треугольник ABD с острыми углами 60 и 30 градусов.
Сторона АВ прямоугольника противолежит углу 30 градусов и равна половине диагонали.
АВ+АD=(2√3+2):2=√3+1
Пусть АВ=х, тогда
АD=(√3+1)-х
АВ:AD=tg 30=1/√3
х:((√3+1)-х)=1/√3
х√3=(√3+1)-х
х√3+х=(√3+1)
х(√3+1)=(√3+1)
х=1
АВ=1
АD=2AB=2