Дано: СИ
R = 100 МОм 100*10⁶ Ом
E = 120 В
V = 10 см/с 0,10 м/с
d = 1 мм 1*10⁻³ м
d₀ = 1,1 мм 1,1*10⁻⁶ м
L = 1 м
ε₀ = 8,85*10⁻¹² Ф/м
_____________
I - ?
Решение.
1)
Чертим электрическую схему (рис.1)
Постоянному току конденсатор представляет разрыв цепи.
2)
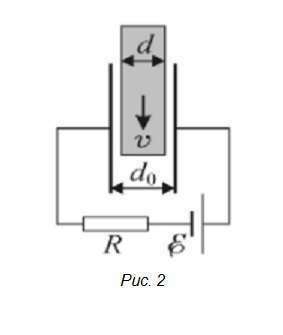
Начинаем вдвигать металлическую пластину. В это случае получаем два конденсатора, соединенных последовательно (рис. 2)
Емкость конденсатора зависит от скорости движения пластины:
C₁(Δt) = ε₀*L*V*Δt / ( (d₀ - d)/2)
(Чтобы не загромождать решение, подставим данные):
C₁(Δt) = 8,85*10⁻¹²*1*0,1*Δt / ( ( 1,1*10⁻⁶ - 1,0*10⁻⁶)/2) ≈ 18*10⁻⁶*Δt
При последовательном соединении двух одинаковых конденсаторов емкость батареи уменьшается в 2 раза.
Имеем С(Δt) = 9*10⁻⁶*Δt. (1)
3)
Из определения емкости конденсатора:
C(Δt) = Δq / Uc
Но
Δq = I*Δt
Имеем:
C(Δt) = I*Δt / Uc (2)
Приравниваем (2) и (1):
I*Δt / Uc = 9*10⁻⁶*Δt.
I / Uc = 9*10⁻⁶
Uc = I / 9*10⁻⁶
Uc = 0,11*10⁶ * I
4)
Запишем закон Ома для полной цепи:
E = I*R + Uc
E = I*100*10⁶ + I*0,11*10⁶
120 = I*(100,11*10*⁶)
I = 120 / (100,11*10⁶) ≈ 1,2*10⁻⁶ А или 1,2 мкА