В параллелограмме ABCD, AB=5см, AD=8см, угол B=150 градусов. Найдите: а) Площадь...

Question

В параллелограмме ABCD, AB=5см, AD=8см, угол B=150 градусов. Найдите: а) Площадь параллелограмма; б) Высоту, проведенную к большей стороне.

Answer 1

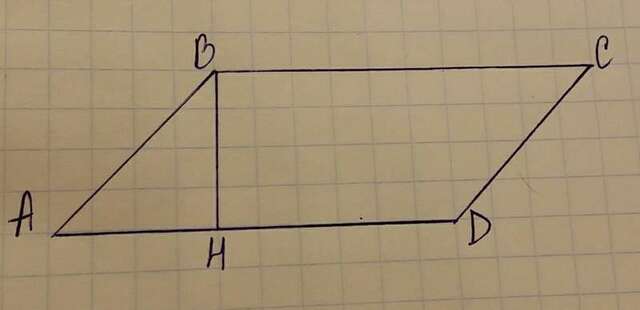
Дано: АВСD - параллелограмм, АВ=5см, AD=8см; угол В=150°, BH - высота.

Найти: а) Sabcd; б) BH.

Решение:

б) Т.к. угол В=150°, тогда угол А=30° (Т.к. углы односторонние и их сумма равна 180°).
Рассмотрим треугольник ABH, он прямоугольный, потому что ВН - высота.
В данном треугольнике мы можем найти ВН по следующему правилу: в прямоугольном треугольнике напротив угла в 30° лежит сторона равная половине гипотенузы, значит ВН=5÷2=2,5см

а) S=AD*BH
S=2,5*8=20см^2

---

Answer 2

Проведем высоту BK┴AD. Угол BAD=180-150=30(градусов). Рассмотрим прямоугольный треугольник ABK:

 BK - катет лежащий против угла в 30 (градусов), следовательно BK равен половине гипотинузы AB, то есть 2,5. 

Площадь параллелограмма равна= BK*BC=2,5*8=20(см^2)