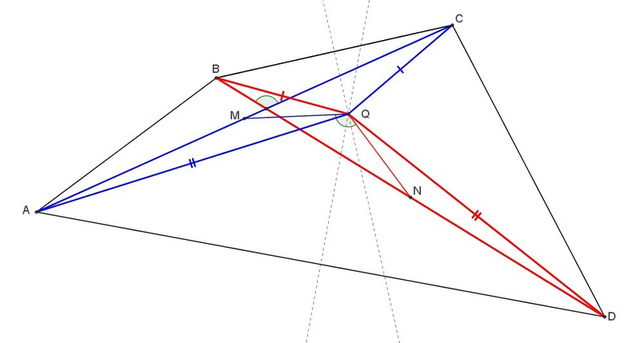
Имеются. Например, если в четырехугольнике ABCD диагонали равны, серединные перпендикуляры к отрезкам BC и AD пересекаются в точке Q, а М и N - середины диагоналей AC и BD соответственно, то QN=QM и ∠NQM равен углу между диагоналями четырехугольника.
Действительно, треугольники AQC и DQB очевидно равны по трем сторонам, а значит совмещаются поворотом вокруг точки Q (синий и красный треугольники). Значит их медианы QN и QM тоже совместятся при этом повороте, т.е. QN=QM и ∠MQN равен углу между прямыми AC и DB (т.к. диагональ AC переходит в DB).