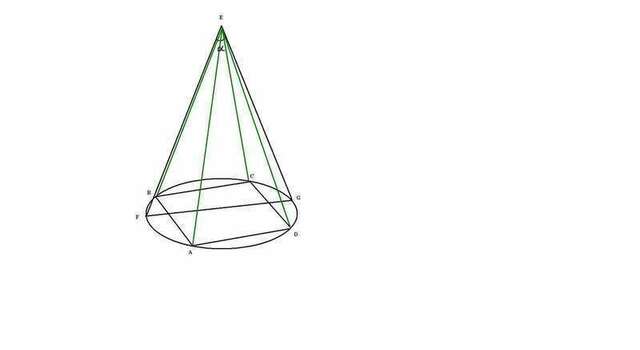
1)  квадрат
квадрат 
 - диаметр окружности.
- диаметр окружности.

Так как 

Найдем высоту грани , так как в оснований квадрат , то по Теореме Пифагора

Тогда площади всех четырех граней равна

2)Ведро имеет форму усеченного конуса , его развертка будет что то трубы . окружность с радиусом равным 20 см , имеет длину окружности
 см = 62,8 см
см = 62,8 см
окружность с радиусом равным 28 , имеет длину окружности
 = 87,92 см
= 87,92 см
Теперь, найдем длину образующей, умножая затем ее на 2 получим первое измерение трубы, второй будет 87.92 см

имеет измерение  см
см
Найдем теперь площадь этой полуокружности , ее диаметр будет равен
 см
см
 см
см
 см ^2
см ^2
 дм^2
дм^2