Определения:
1. Прямая и плоскость называются параллельными, если они не имеют общих точек.
2. Две плоскости называются параллельными, если они не имеют общих точек.
3. Две параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.
4. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
Следствие из аксиом стереометрии: через две пересекающиеся прямые проходит плоскость и притом только одна.
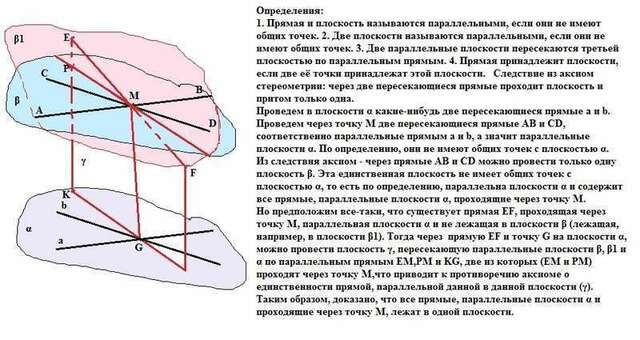
Проведем в плоскости α какие-нибудь две пересекающиеся прямые а и b. Проведем через точку М две пересекающиеся прямые АВ и СD, соответственно параллельные прямым a и b, а значит параллельные плоскости α.
По определению, они не имеют общих точек с плоскостью α.
Из следствия аксиом - через прямые АВ и CD можно провести только одну плоскость β. Эта единственная плоскость не имеет общих точек с плоскостью α, то есть по определению, параллельна плоскости α и содержит все прямые, параллельные плоскости α, проходящие через точку М.
Но предположим все-таки, что существует прямая EF, проходящая через точку М, параллельная плоскости α и не лежащая в плоскости β (лежащая, например, в плоскости β1). Тогда через прямую EF и точку G на плоскости α, можно провести плоскость γ, пересекающую параллельные плоскости β, β1 и α по параллельным прямым ЕМ,РМ и KG, две из которых (EM и РМ) проходят через точку М,что приводит к противоречию аксиоме о единственности прямой, параллельной данной в данной плоскости (γ).
Таким образом, доказано, что все прямые, параллельные плоскости α и проходящие через точку М, лежат в одной плоскости.