Дано;
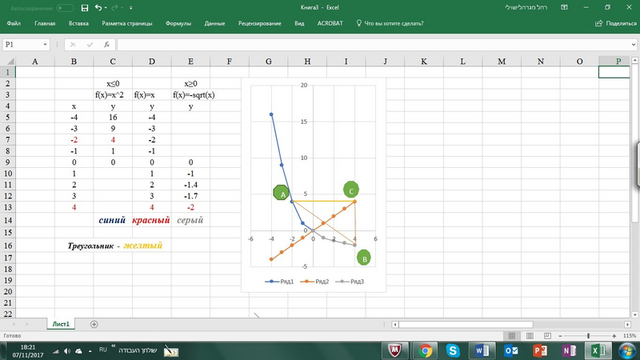
Вершины Δ АСВ: А(-2;4), С(4;4), В(4;-2)
Точки принадлежат функции: А(-2;4) - f(x)=x²
C(4;4) - f(x)=x
B(4;-2) - f(x)=√x
Найти длину сторон;
АВ=√((-2-4)²+(4+2)²)=√(36+36)=√72
АС=√((-2-4)²+(4-4)²)=√36
ВС=√((4-4)²+(-2-4)²=√36
Δ АСВ - равнобедренный: АС=ВС=6
Доказательства, что Δ АСВ - прямой:
1. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гепотенузы: (√36)²+(√36)²=(√72)²
36+36=72 - ∠АСВ - прямой.
2. В равнобедренном Δ углы, прилегающие к гипотенузе равны 45°:
∠САВ=∠СВА=45°
180°-45°-45°=90° - ∠АСВ=90° - прямой.
График во вложении