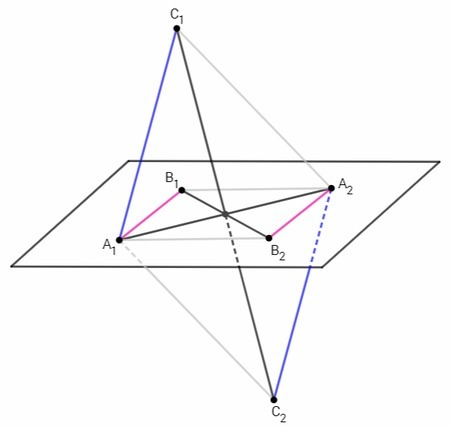
Через две пересекающиеся прямые можно провести плоскость, притом только одну. Пересекающиеся отрезки являются частями пересекающихся прямых. Вершины двух пересекающихся отрезков лежат в одной плоскости и образуют четырехугольник.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то четырехугольник является параллелограммом. Так как данные отрезки точкой пересечения делятся пополам, образуемый их вершинами четырехугольник является параллелограммом.
A1B1A2B2, A1C1A2C2 - параллелограммы.
Противоположные стороны параллелограммов параллельны.
A1B1 || A2B2, A1C1 || A2C2
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны. Пересекающиеся прямые A1B1 и A1C1, лежащие в плоскости A1B1C1, параллельны пересекающимся прямым A2B2 и A2C2, лежащим в плоскости A2B2C2. Следовательно, плоскость A1B1C1 параллельна плоскости A2B2C2.