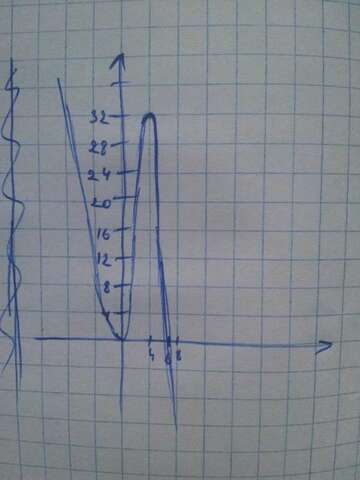
У=-х^3+6х^2
D(f) = R
E(f) = R
y(-x) = -(-x)^3+6(-x)^2= +x^3+6x^2 (функция общего вида)
у(0) =0^3+6*0^2=0 (x=0)
-x^3+6x^2=0 (y=0)
6x^2-x^3=0
x^2(6-x)=0
x=0 6-x=0
x=6 (в точках 0 и 6 график пересекает ось ох)
(теперь находим производную и приравниваем к 0)
f '(x) = -3x^2+12x
-3x^2+12x=0
12x-3x^2=0
3x(4-x)=0
x=0 4-x=0
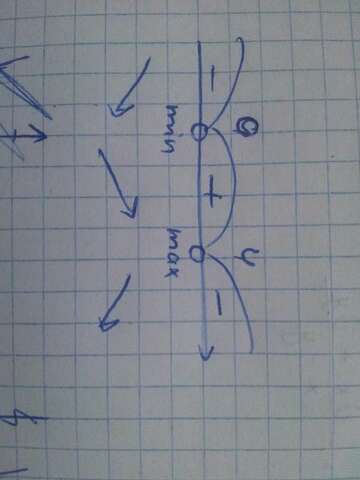
возрастает [0,4]
убывает (-∞,0] [4,+∞)
x max = 4 y max = 32 (y(5)= -4^3+6*4^2=-64+96=32)
x min = 0 y min = 0