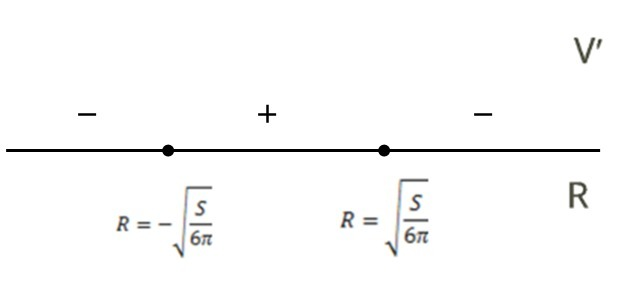Из всех геометрических тел с заданной площадью поверхности максимальный объем будет у шара...))
Поскольку задан цилиндр, то, в этом случае, максимальный объем будет у цилиндра с квадратным вертикальным сечением, т.е. R = H/2
Докажем это:
Площадь полной поверхности цилиндра можно вычислить по формуле:
S = 2πR² + 2πRH - Выразим из этой формулы H:
2πRH = S - 2πR²
H = (S-2πR²)/2πR
Подставим полученное выражение в формулу вычисления объёма цилиндра:
V = πR²H = πR²(S-2πR²)/2πR = SR/2 - πR³
Найдём максимум этой функции одной переменной. Для этого вычислим производную и приравняем к нулю:
V′ = (SR/2 - πR³)′ = S/2 - 3πR²
S/2 - 3πR² = 0
R² = S/6π
R = √(S/6π)
R = -√(S/6π)
Отметим эти значения на координатной прямой и определим знак производной на трёх полученных числовых интервалах: (см. рис.)
Известно, что в точке максимума производная меняет знак с плюса на
минус. Соответственно, максимальный объём цилиндра можно получить, если
радиус основания цилиндра будет равен:
R = √(S/6π)
Максимальный объём цилиндра:
V = SR/2 - πR³ = R(S/2 - πR²) = √(S/6π) *(S/2 - S/6) =
= √(S/6π) * S/3
Найдем высоту цилиндра:
S = 2πR(R+H) => H = S/2πR - R = S/2π(√(S/6π)) - √(S/6π) =
= √(6πS)/3π
Так как: R = √(S/6π) = √(6πS)/6π, то R = H/2