(над всем ставим чёрточки векторов, я не имею технической возможности это сделать)
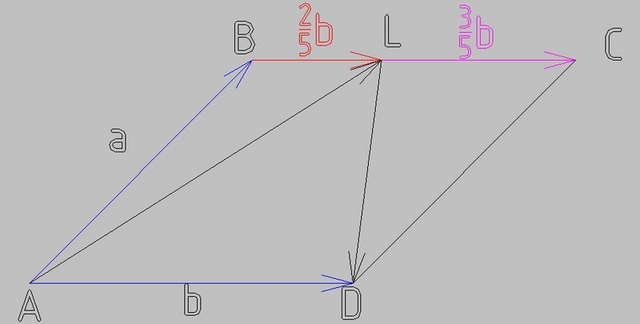
1. ВС = AD = b
2. Из того, что BL:LC=2:3 следует, что
BL = 2/5 b (красное на рисунке) и
LC = 3/5 b (малиновое)
Теперь можно заняться решением заданных вопросов
3. По правилу сложения векторов
AL = AB + BL = a + 2/5 b
4. Снова складываем вектора
CD = BA = -a
LD = LC + СD = 3/5 b - a
Или, второй вариант решения.
AL + LD = AD
LD = AD - AL
AL мы вычислили в прошлом пункте
LD = b - AL = b - a - 2/5 b = 3/5 b - a