13)
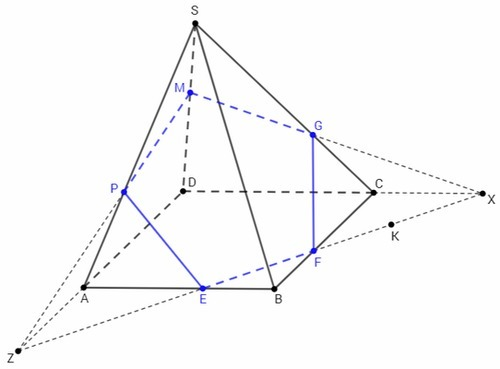
PM лежит в плоскости (ADS) и пересекает AD в точке Z.
ZK лежит в плоскости (ABCD) и пересекает AB в точке E, BC в точке F, CD в точке X.
XM лежит в плоскости (CDS) и пересекает CS в точке G.
EFGMP - сечение данной пирамиды полоскостью (PMK).
14)
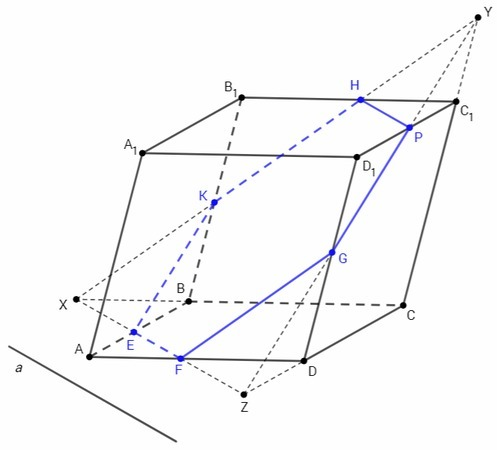
Через точку E в плоскости (ABCD) проведем прямую EF, параллельную a.
EF пересекает BC в точке X, AD в точке F, CD в точке Z.
ZP лежит в плоскости (DD1CC1) и пересекает DD1 в точке G, CC1 в точке Y.
XY лежит в плоскости (BB1CC1) и пересекает BB1 в точке K, B1C1 в точке H.
Прямая а, не лежащая в плоскости сечения*, параллельна прямой EF, лежащей в плоскости сечения, следовательно прямая а параллельна плоскости сечения.
EFGPHK - сечение данного параллелепипеда плоскостью, параллельной прямой а.
-----------------------------------------------
*) Плоскость (ABCD) и плоскость сечения пересекаются по прямой EF. Прямая EF проведена через точку E, не принадлежащую прямой а, следовательно EF не совпадает с a. Две пересекающиеся плоскости могут иметь только одну общую прямую, следовательно прямая а не лежит в плоскости сечения.