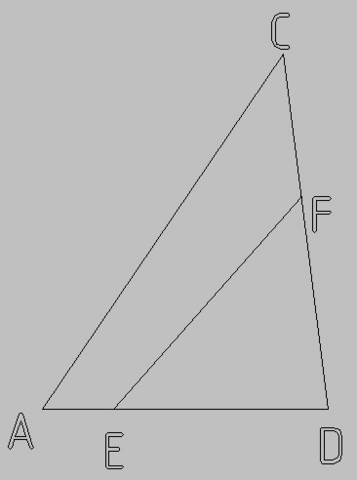
Координатный метод
A(0,0)
D(4,0)
C(x₁,y₁)
AC = √(x₁²+y₁²) = 6
CD = √((x₁-4)²+y₁²) = 5
---
x₁²+y₁² = 36
(x₁-4)²+y₁² = 25
---
x₁²+y₁² = 36
x₁²-8x₁+16+y₁² = 25
---
вычтем второе из первого
8x₁-16 = 36-25
8x₁-16 = 11
8x₁ = 11+16 = 27
x₁ = 27/8
x₁²+y₁² = 36
(27/8)²+y₁² = 36
y₁² = 36 - 729/64
y₁² = 1575/64
y₁ = 15√7/8
Отрицательный корень отбросим, нам вторая точка пересечения не нужна
C(27/8;15√7/8)
----------------------------------
(вектор)AC = С-A = (27/8;15√7/8)
(вектор)FC = 2/5(вектор)DC = 2/5(С-D) = 2/5(27/8-4;15√7/8) = 2/5(-5/8;15√7/8) = (-1/4;3√7/4)
Надо найти координаты точки F
(вектор)FC = C-F
F = C-(вектор)FC = (27/8;15√7/8) - (-1/4;3√7/4) = (29/8;9√7/8)
Е(1;0)
(вектор)FE = E-F = (1-29/8;0-9√7/8) = (-21/8;-9√7/8)
---------------
(вектор){AC +FC+ FE} = (27/8;15√7/8)+(-1/4;3√7/4)+(-21/8;-9√7/8) = (27/8-1/4-21/8;15√7/8+3√7/4-9√7/8) = (1/2;3√7/2)
|AC +FC+ FE| = √((1/2)²+(3√7/2)²) = √(1/4+9*7/4) = √(1/4+63/4) = √(64/4) = √16 = 4