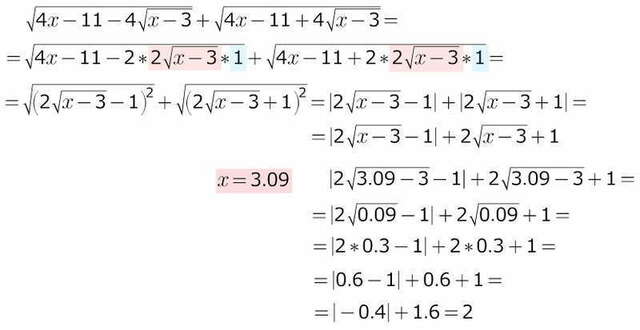Под одним корнем --квадрат разности, под другим --квадрат суммы...
корни извлекаются)) второй корень извлекается однозначно (там под корнем остается всегда неотрицательное число) а вот первый корень может быть равен только неотрицательному числу (по определению), потому модуль сохраняется...
напомню формулу: √(х²) = |x|