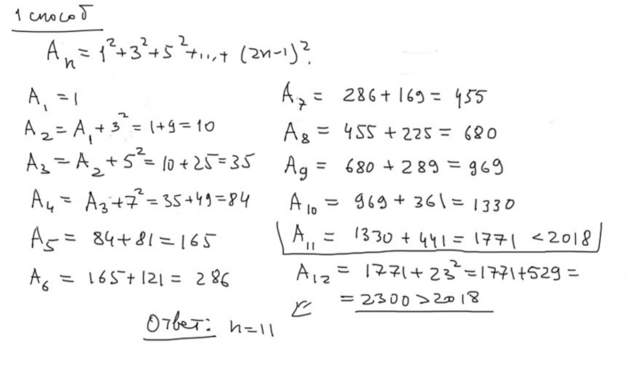В картинках два способа.
1-ый способ: посчитать "в лоб" все суммы до n=12. Это довольно быстро.
2-ой способ длиннее, зато "высокоинтеллектуальный" :) и годится для чисел существенно больших 2018.
1) Вначале выводим общую формулу для суммы (можно не выводить, если помните ее) S[n]=1²+2²+3²+...+n²=n(n+1)(2n+1)/6.
2) Потом из нее выводим формулу для суммы из левой части условия: 1²+3²+5²+...+(2n-1)²=S[2n]-4S[n]=n(4n²-1)/3.
3) Затем легко прикинуть, что если эта сумма около 2018, то n около 11.
4) Проверяем n=11 и 12 и находим n=11.