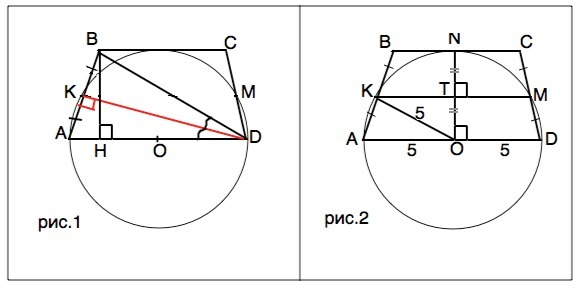
АКМD - трапеция, вписанная в окружность.
Вписать в окружность можно только равнобедренную трапецию, ⇒
АВСD также равнобедренная трапеция.
КМ хорда данной окружности и средняя линия трапеции, поэтому параллельна АD
а) См. рис.1 вложения.
Высота АВСD равна длине отрезка, проведенного из центра в точку касания, т.е. равна радиусу окружности.
ВН=d:2=10:2=5.
Соединим К и D
В ∆ АКD вписанный угол AКD опирается на диаметр и равен 90°. Смежный ему угол ВКD=90°
В ∆ АВD AK=KB, DK⊥АВ, ⇒ отрезок KD – медиана и высота.
Следовательно, ∆ АВD равнобедренный, ВD=AD=10
Формула площади треугольника S=ab:2
2S (ABD)=BH•AD=5•10=50
Другая формула площади треугольника
S=a•b•sinα:2, где a и b – стороны треугольника, α – угол между ними.
sinα=2S:ab=50:100=1/2 - это синус 30°
Углы при основании равнобедренного треугольника равны.
∠АВD=∠ВАD=(180°-30°):2=75°
———
б) См. рис.2.
Радиус ОN перпендикулярен хорде КМ и делит её пополам. ⇒
КТ=ТМ= (свойство).
∆ АКО – равнобедренный. Углы при основании АК из доказанного выше =75°
Тогда ∠КОА=180°-2•75°=30°,
и угол КОТ=

KM=2•5√3/2=5√3 (ед. длины)