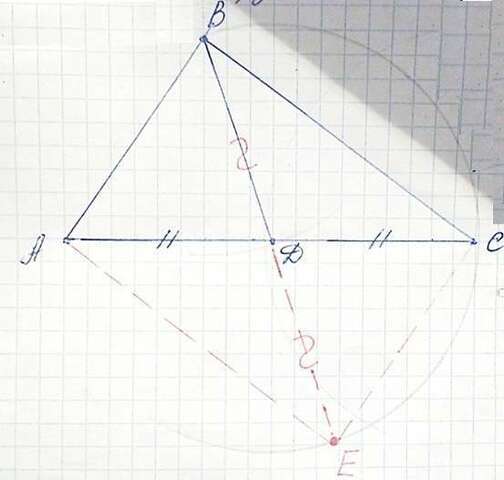
Проведем из точки
D окружность с радиусом BD.
На пересечении
луча из точки B и окружности обозначим точку Е.
Т.к. диагонали образовавшегося четырехугольника ABCE (достроили
красным пунктиром) в точке пересечения D деляться пополам ( AD=DC, т.к. BD - медиана, а BD=DE по условиям задачи), то
четырёхугольник ABCE является параллелограммом, согласно
свойства диагоналей параллелограмма (Диагонали параллелограмма точкой
пересечения делятся пополам).
Следовательно AB=CE=5.8см,
исходя из определения: «Параллелограммом
называется четырехугольник, у которого противоположные стороны попарно
параллельны».
ПРОВЕРКА (есть
небольшие погрешности в сотых).
BD²=( 2*AB²+
2*BC²-
AC²):4=(2*5,8²+2*7,4²-9²)÷4
BD =4,9
BE²*AC²=2*(CE²+BC²).
CE²= ((BE²*AC²):2)- BC²
CE²=((9,8²+9²)÷2)- 7,4²=((96+81)÷2)-54,8=33,7
CE=5,8