Равнобедренный треугольник ABC (AB=BC=6) повернуть ** угол 45 градусов вокруг точки A...

Question

Равнобедренный треугольник ABC (AB=BC=6) повернуть на угол 45 градусов вокруг точки A (рис.). Точка B перешла в точку B1, точка C-в точку C1, при этом точка С оказалась на отрезке B1C1. Найти периметр треугольника B1KC.

---

Answer 1

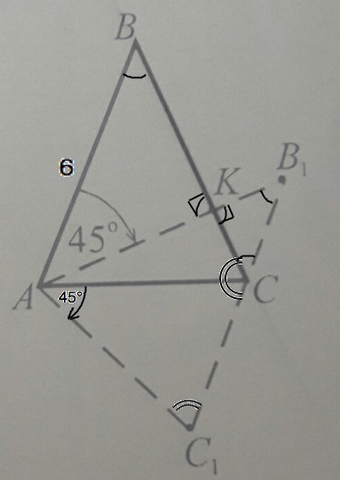
В ∆ АВС  АВ=ВС=6 см, 

Угол ВАВ1 = 45°⇒

 Угол САС1=45° 

АС перешло в АС1 ⇒ АС=АС1⇒ 

∆ АСС1  равнобедренный. 

∠АС1С=∠АСС1. ∠АС1С=∠АСВ⇒

∠АВС=∠САС1=45° ⇒

В ∆ АВК два угла равны 45° ⇒ ∆ АВК - прямоугольный. 

ВК=АВ•sin45°=3√2

∆ ВКС прямоугольный ( угол В1КС равен углу ВКА как вертикальный). 

В ∆ СКВ1 катеты КВ1=КС=ВС- ВК=6-3√2

В1С=KC:sin45°=(6-3√2)•√2=6√2-6

Р ∆ КСВ1=6-3√2+6-3√2+6√2-6=6 ед. длины. 

---