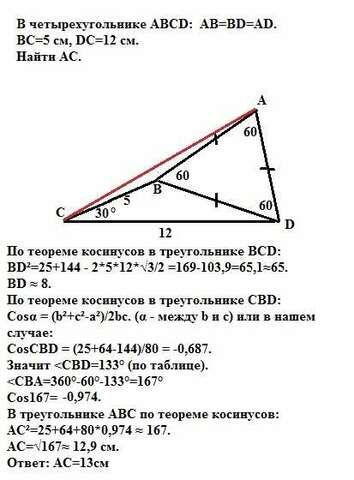
По теореме косинусов в треугольнике ВСD:
ВD²=25+144 - 2*5*12*√3/2 =169-103,9=65,1≈65.
BD ≈ 8.
По теореме косинусов в треугольнике СВD:
Cosα = (b²+c²-a²)/2bc. (α - между b и c) или в нашем случае:
CosCBD = (25+64-144)/80 = -0,687.
Значит Cos167= -0,974.
В треугольнике АВС по теореме косинусов:
АС²=25+64+80*0,974 ≈ 167.
АС=√167≈ 12,9 см.
Ответ: АС=13см.