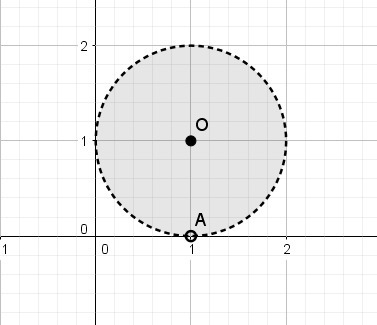
Первое неравенство системы можно записать как (х-1)²+(y-1)²<1, т.е. оно задает круг, радиуса 1 и с центром в О(1;1). При этом граница круга не включается, т.к. неравенство строгое.<br>
Второе условие (x-1)²+y²≠0 задает всю плоскость кроме точки А(1;0). Действительно, противоположное условие к нему было бы (x-1)²+y²=0, что выполняется только для точки А(1;0) (т.к. сумма квадратов может быть равна 0 только, если каждое слагаемое равно 0).
Итак, пересечение этих множеств дает только круг соответсвующий первому неравенству системы не включая точку А. Т.к. точка А лежит на границе круга, которая, согласно первому неравенству системы, не принадлежит искомому множеству, то выколотую точку А можно было и не рисовать.