1) Рассмотрим рис.1 вложения
Трапеция равнобедренная, т.к.
в окружность можно вписать только равнобедренную трапецию.
ВК=ВД по условию, АВ=СД как боковые стороны равнобедренной трапеции.
В окружности равные хорды опираются на равные дуги. .
Равные хорды ВК и ВД опираются на равные дуги, следовательно, на равные дуги опираются вписанные углы ВАК и ВСД.
Вписанные углы, опирающиеся на равные дуги, равны.
Вписанные углы АКВ и СВД опираются на равные дуги и потому равны.
В треугольниках АВК и СВД по два равных угла, следовательно, равны в них и углы АВК и ВДС ( на рисунке равные углы окрашены в одинаковый цвет).
В этих треугольниках между равным сторонами АВ = ДС и ВК = ВД содержатся равные углы - отсюда эти треугольники равны.
АК=ВС=4 см
--------------------------------------
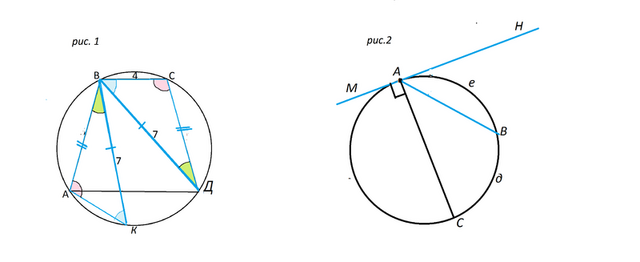
2) Сделаем рисунок. Во вложении это рис.2
Пусть касательная к окружности будет МН, точка касания А, хорда, имеющая с касательной общую точку на окружности, АВ.
Проведем через центр окружности ещё одну хорду с общей точкой с касательной в точке А. Эта хорда - диаметр АС.
Угол САН - прямой ( диаметр к точке касания перпендикулярен касательной) и равен половине дуги АеВдС, которая равна 180 градусов
Угол НАС равен сумме углов САВ и ВАН, равен половине градусной меры дуги СдВеА и равен 90 градусам.
Дуга АеВдС равна сумме дуг ВдС и ВеА
Угол САВ, как вписанный, равен половине градусной меры дуги ВдС
Так как половины дуг АеВ и ВдС в сумме равны 90 градусам, угол НАВ равен половине градусной меры дуги АеВ, что и требовалось доказать.