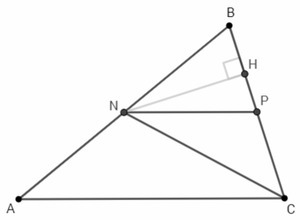
Площадь треугольника, отсекаемого средней линией, равна четверти площади исходного треугольника*. S(NPB)=40/4=10. Треугольники NPB и NPC имеют общую высоту (опущенную из N на BC) и равные основания (BP=PC), следовательно их площади равны. S(NPC)=S(NPB)=10.
----------------------------------------------------
*) Средняя линия равна половине основания. Средняя линия делит высоту (и любой отрезок, соединяющий противолежащую вершину и точку на параллельном основании) пополам. Произведение половины основания и половины высоты дает вчетверо меньшую площадь.