Вычеслить площадь фигуры, ограниченной линиями y=x^2 и y=1

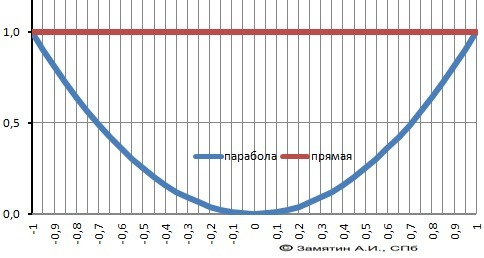
РЕШЕНИЕ
Площадь - интеграл разности функций.
Находим пределы интегрирования.
x² = 1, а= 1, b = -1.
Составляем функцию площади
$S=\int\limits^1_b {(1-x^2)} \, dx= \frac{x}{1}- \frac{x^3}{3}$
Вычисляем значения на границах интегрирования.
S = S(1) - S(-1) = 2/3 - (-2/3) = 1 1/3 - площадь - ОТВЕТ
Рисунок к задаче в приложении.