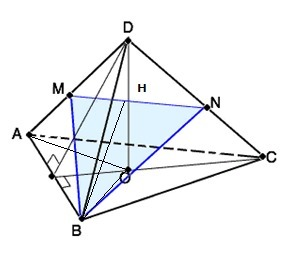
1. Для наглядности сделаем вот
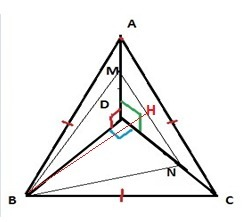
такой рисунок. На нашем рисунке пирамида положена на боковую
грань. Перпендикулярные грани нам видны. Видим основание
пирамиды- равносторонний треугольник, так как по условию АВ=ВС=АС.
Рассмотрим ΔADB, ΔADC.
AB=AC, ∠ADB=∠ADC=90°- по условию. AD-общий катет⇒
прямоугольные ΔADB=ΔADC
Рассмотрим ΔADC, ΔBDC.
AC=BC, ∠ADC=∠BDC=90° -по условию, DC-общий катет⇒
прямоугольные ΔADC=ΔBDC.
Рассмотрим ΔBDC и ΔADB.
CB=AB, ∠BDC=∠ADB=90° -по условию, DB-общий катет⇒
прямоугольные ΔBDC=ΔADB ⇒
AD=DC=DB-боковые ребра пирамиды равны, боковые грани- равнобедренные равные треугольники ΔADB=ΔADC=ΔBDC⇒вершина пирамиды проецируется в центр ΔABC (если ребра равны, их проекции также равны)⇒ АВСD-правильная пирамида.
2. Рассмотрим ΔАDС. АD=DС как ребра правильной пирамиды, значит
ΔАDС-равнобедренный.
DM:MA=DN:NC=3:2, значит ΔDMN подобен ΔADC.
DN :MN =DC :AC ⇒
3/MN=5/10
MN=3*10/5=6
AC²=2DC²⇒ DC=√AC²/2=√50=5√2,
тогда DN=5√2/5*3=3√2
BD=DC BN=√(BD²+DN²)=√25*2+9*2=2√17
Опустим
высоту ВН на основание MN
BH=√(BN²-HN²)=√(4*17-3²)=√68-9=√59
S BMN=1/2BH*MN=1/2*6*√59=3√59
Ответ: S BMN=3√59