Номер 7.
Тут достаточно вспомнить формулу разности квадратов:
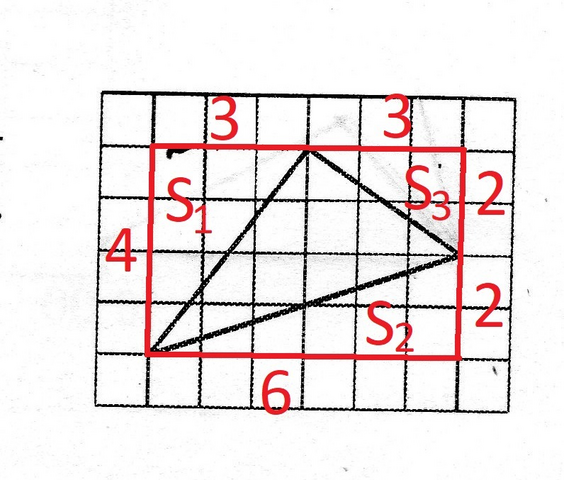
 Номер 11. (см рисунок)
Номер 11. (см рисунок)
Тут можно найти площадь прямоугольника. Вычесть из него площадь маленьких треугольников S1, S2 и S3 и выйдет площадь искомого треугольника.
Площадь квадрата:

Площади 3-х маленьких треугольников:

Тогда, площадь искомого треугольника: