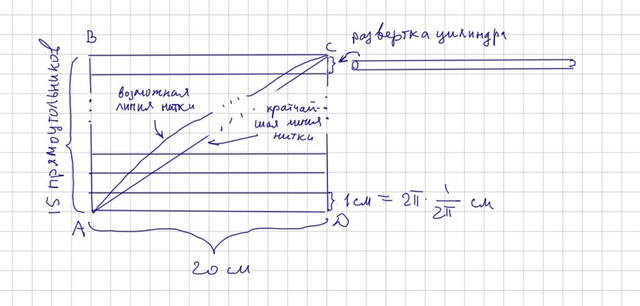
Если развернуть поверхность цилиндра (стержня) на плоскость, то получится прямоугольник со сторонами 20 см. и 2π·(1/(2π))=1 см. Т.к. нитка совершила ровно 15 оборотов, то, составляя 15 таких разверток вместе, получим прямоугольник ABCD со сторонами 20 см. и 15 см., а линия нитки развернется в линию, соединяющую его диагональные вершины А и С (т.к. начинается на одном конце стержня, а заканчивается на другом, см. рисунок). На каждой очередной развертке показан соответствующий виток нитки. Минимальное расстояние между точками А и С равно длине отрезка AC, поэтому по т. Пифагора минимальная длина нитки равна √(20²+15²)=25.