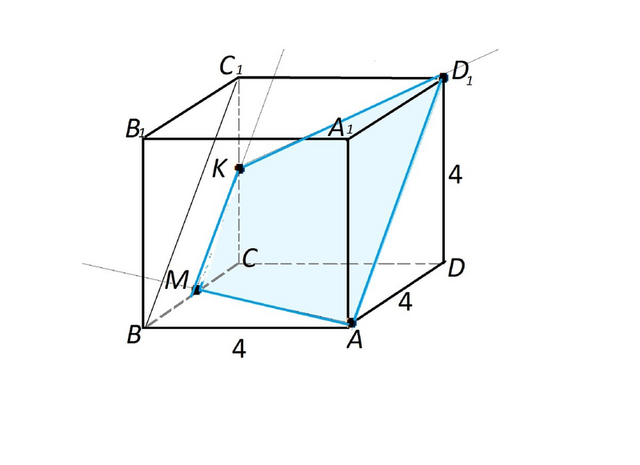
Через две точки можно провести прямую, если эти точки лежат в одной плоскости.
Здесь А и Д лежат в одной плоскости, поэтому через них можно провести прямую. Соединим их.
А и М тоже лежат в одной плоскости, соединим их.
Плоскость (BCC₁) параллельна плоскости (ADD₁),поэтому через М проводим прямую параллельно DD1.
Она пересеклась с СС1. Обозначим точку их пересечения К.
Точки К и D₁ лежат в одной плоскости, ⇒ через них можно провести прямую, лежащую в этой плоскости.
Получено нужное сечение АМКD₁.
Для того, чтобы вычислить периметр сечения, нужно найти длину всех стороны четырехугольника АМКD₁
АD₁ - диагональ квадрата со стороной 4
АD₁=4√2
МК параллельна ВС₁=AD₁ и является средней линией треугольника ВСС₁.
Она равна половине ВС₁
МК=2√2
⊿АВМ=⊿КС₁D₁ по двум сторонам и углу между ними.
АМ=КD₁
Из треугольника АВМ, где АВ=4, ВА=2
АМ=√(АВ²+ВМ²)=√(16+4)=2√5
Периметр АМКD₁
Р=2*2√5+4√2+2√2Р=6√2+4√5 (единиц длины)