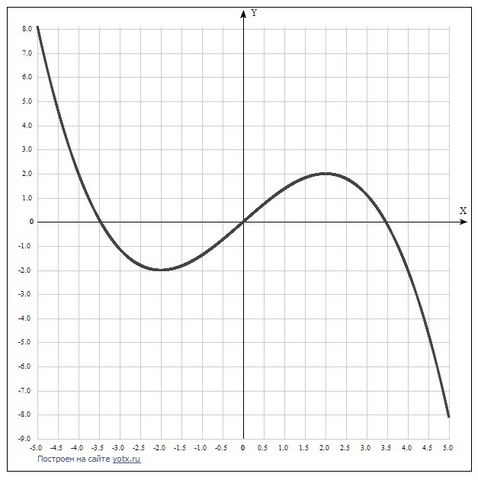
Дана функция y=1/8(12x-x^3).
Её также можно представить в виде: у=(-1/8)x³ + (3/2)х.
1.Найти область определения функции.
Для этой функции нет ограничений, поэтому D ∈ R (действительные числа).
2.Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.
f(-x) =(1/8)x³ - (3/2)x = -((-1/8)x + (3/2)x) = -f(x). Функция нечётная.
Она также не периодическая.
3.Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства функции.
График функции пересекает ось X при f = 0, значит надо решить уравнение: (-1/8)x³ + (3/2)х = 0.
(-1/8)x*(x² - 12) = 0.
Имеем 3 корня этого уравнения: х = 0, х = √12 = 2√3 и х = -2√3.
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в (12*x - x^3)/8 = (12*0 -0³)/8 = 0.
Точка: (0, 0)
4.Найти производную функции и ее критические точки.
Для того, чтобы найти критические точки, нужно найти производную и приравнять её нулю.
Первая производная y' = (-3/8)(x² - 4).
Решаем это уравнение: x = +-√4 = +-2.
Значит, критические точки: (-2, -2), (2, 2).
5.Найти промежутки монотонности и экстремумы функции.
Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где
производная с плюса меняется на минус - точка максимума, а где с минуса на плюс
- точки минимума.
Находим значения производной в промежутках между критическими точками и нулём (третья точка) - всего 4 промежутка.
x =
-3
-2 -1 0
1 2 3
y' =
-1,875
0 1,125 1,5 1,125 0
-1,875.
Интервалы возрастания и убывания функции:
Возрастает на промежутке ( -2; 2),
Убывает на промежутках (-oo, -2] U [2, oo).
Минимум функции в точке (-2; -2), максимум функции в точке (2; 2).
6.Построить график функции, используя полученные результаты исследования - дан в приложении.
Координаты точек для построения графика:
xy-5.0 8.13, -4.5 4.64, -4.0 2, -3.5 0.11,-3.0 -1.12, -2.5 -1.8, -2.0 -2, -1.5 -1.83, -1.0 -1.37, -0.5 -0.73, 0, 0.5 0.73,1.0 .38,1.5 1.83, 2.0 2, 2.5 1.8, 3.0 1.13, 3.5 -0.11, 4.0 -2, 4.5 -4.64, 5.0 -8.12