Найдите 3 непоределённых интеграла и вычислите площадь 1 фигуры, ограниченной пораболами

ЗАДАЧА
Площадь фигуры
Y1= -x² + x + 5
Y2 = 2x² + 6x - 3
РЕШЕНИЕ
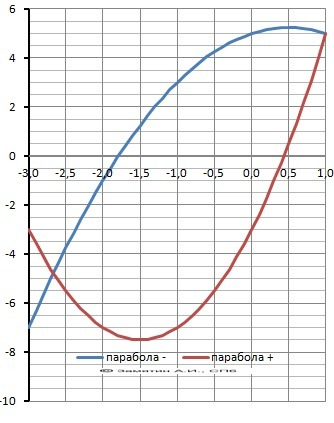
Графическое решение на рисунке в приложении.
1) Пределы интегрирования - разность функций равна 0.
F = Y1 - Y2 = - 3x²- 5x + 8 = 0
Решаем квадратное уравнение
D =121, a = 1, b = - 2 2/3
Площадь фигуры и есть интеграл функции F. Под интегралом удобнее записать в обратном порядке..
$S=\int\limits^1_b {F(x)} \, dx= \int\limits^1_b {(8-5x-3x^2)} \, dx= \\ =\frac{8}{1}- \frac{5x}{2}- \frac{3x^2}{3}= 4 \frac{1}{2} -(-20 \frac{1}{7})=24 \frac{35}{54}$
Вычисляем на границах интегрирования
S(1) = 8 - 2?5 - 1 = 4,5
S(-2 2/3) = -21 1/3 - 17 7/9 + 18 26/27 = - 20 4/27
ОТВЕТ ≈24,65