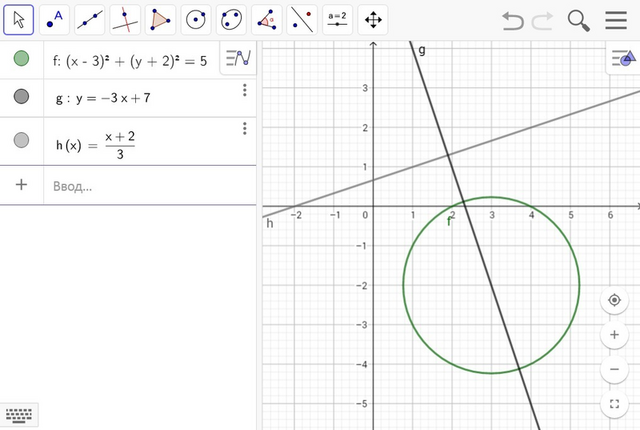
Перепишем уравнение прямой x + 2 = 3y:
y = x/3 + 2/3.
Здесь k1 = 1/3, b1 = 2/3.
Перепишем уравнение окружности:
x*x - 6x + 9 + y*y + 4y + 4 - 5 = 0,
(x - 3)^2 + (y + 2)^2 = 5.
Это окружность с радиусом, равным sqrt(5) (корень квадратный из пяти).
Коеффициент k2 искомой функции, которая перпендикулярна к прямой x-3y+2=0 будет -(1/k1), т. е. -3.
Искомая функция y3 = -3x + b2.
Ее график проходит через центр окружности, координаты которого (3, -2), что мы получили из уравнения круга.
y3 = -2 = -3*3 + b2 = -9 + b2
b2 = 7
Ответ: y3 = -3*x + 7